|
One,
two, three and away you go. Or should I say one, three,
five. If you want to understand how chords derive their
notes and names all you need is some systematic thinking
and a scale. The numbers game is an essential part of this
process and when you finally grasp the idea, it's very enlightening
and surprisingly simple.
Our
template for this concept is C Major, the mother of all
scales;
C
D E F G A B C.
If
you look carefully you'l notice there's only seven different
letters. And to see it in text doesn't give you much to
go on because it's just an alphabetical series of notes
but there's way more there than meets the eye. In fact it's
loaded with hidden goodies that affect tons of other musical
theories. For this page we'll have a look at a couple of
the more pertinant elements.
First
we'll get back to the numbers thing. Simply put, if we call
'C' number 1 then 'D' is number 2, 'E' number 3 and likewise
on through the rest.

As
you can see, if you continue the sequence past 'C'
you wind up with higher numbers such as 9, 10, 11 etc. (Ever
wonder where those numbers in chords come from?) Nonetheless,
you can always consider your first note, in this case 'C',
number 1 even if you repeat past it.

Secondly
we have a limited number of notes to deal with. Consider
them a family. No matter how you look at it, it'll always
be just those notes. And the head of the family, or most
important note of all, is 'C'.
Keeping
those two things in mind, this leads us to the critical
element that drives the whole concept; to manufacture basic
chords or triads as they're called, you can count any
note in that family as number 1!
Confused?
Don't worry, I'll try to clarify.
We'll
take advantage of a nifty little system involving ones,
threes and fives. Once again start on 'C' and call it number
1. From there count up to the third note and that would
be ..... 'E'. Continue on and count up to the fifth note,
use your fingers if you must, and that's (drum roll please)
..... 'G'! For a grand total of C E G.

Next,
start on 'D' and call that number 1. From 'D' count
up to find the third note, 'F', and the fifth, 'A', for
a total of D F A.

Now
start on 'E' and call that number 1. See a pattern developing
here? Count up "a third" to find 'G' and up "a
fifth" to find 'B' for E G B.

As
you go through each note in turn you'll wind up with seven
groups of three notes, one for each different letter, and
then the process repeats itself. These are the triads which
constitute the most basic chords in the key of C. In traditional
notation you'd see them arranged like this:
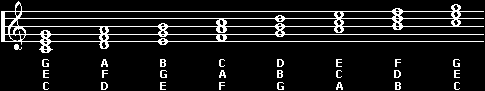
Another
cool thing about this system is the chordal value
of each group.
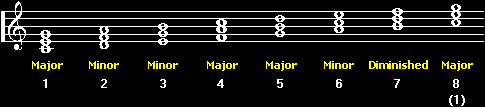
This
is a predictable series of chords no matter which major
key you work with. In other words, the first or key chord
is always major, the second is always minor, the third always
minor, the fourth major, fifth major, sixth minor and the
seventh chord always diminished. In short: major, minor,
minor, major, major, minor, diinished. That's a wonderful
thing to be able to take advantage of because it means you
don't have to learn an entirely new set of chords for a
different key! Just apply the appropriate sharps or flats
relevant to the individual notes in that key.
Let's
have a look at the key of 'A' Major which goes A B C# D
E F# G# A;
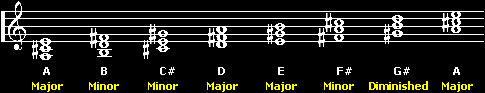
Simply
combine the the note name with the chord type and there
you have it; A major, B minor, C# minor and so on. It's
a beautiful thing to be able to take a simple tool and get
a lot of mileage out of it. And that's just one of many!
The
question now is 'why are some triads major others minor
and what's up with that diminshed thing? And why are they
in that particular order?'.
Sorry
but the answer to that's a subject for another article on
intervals.
It's
important to note that this entire process hinges on some
very logical, well-thought-out mechanisms. Having a firm
grasp of the systems at work and the right tools will eventually
let you build or understand anything musical regardless
of your instrument.
|

